Provided information:
We know the first 4th terms of the series:
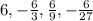
We can express this series in summation notation as:
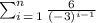
Therefore, the 5th term of the series is:
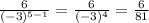
Now, we have to add the first five terms:
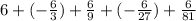
The next step is to convert all fractions to have the same denominator, so:
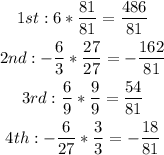
Now, they have the same denominator, it remains the same and we just need to add the numerators:
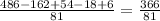
And now, let's simplify the fraction by dividing the numerator and denominator by 3:
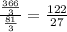
The answer is A. 122/27