Question

Find the derivative of the function y=(4x^ 3 -5x^ 2 )(3x^ 6 +2x^ 5 )10 two different ways. First, multiply the factors togethercollect like terms, then use the basic rules to find the derivative. Second, apply the Product Rule to the function as is currently written.

Answer 1

Given:

The given function is:

`y=(4x^3-5x^2)(3x^6+2x^5)`

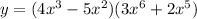
First method: Multiplying factors and differentiating after arranging like terms together.

`\begin{gathered} y=(4x^3-5x^2)(3x^6+2x^5) \\ =4x^3(3x^6+2x^5)-5x^2(3x^6+2x^5) \\ =12x^9+8x^8-15x^8-10x^7 \\ =12x^9-7x^{8^{}}-10x^7 \end{gathered}`

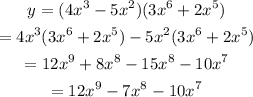
Now we will differentiate y with respect to x by basic rules:

`y^(\prime)=12(9)x^(9-1)-7(8)x^(8-1)-10(7)x^(7-1)`

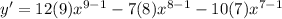
Solving further,

`y^(\prime)=108x^8-56x^7-70x^6`

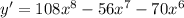
(b) Second method: Apply product rule to find the derivative:

Again,

`y=(4x^3-5x^2)(3x^6+2x^5)`

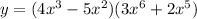
The product rule states:

`(uv)^(\prime)=u^(\prime)v+v^(\prime)u`

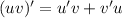
Where u and v are the two factors multiplied.

So here we have:

`\begin{gathered} u=4x^3-5x^2 \\ v=3x^6+2x^5 \end{gathered}`

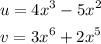
Finding the derivatives:

`\begin{gathered} u^(\prime)=4(3)x^(3-1)-5(2)x^(2-1) \\ =12x^2-10x \end{gathered}`

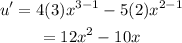
Similarly,

`\begin{gathered} v^(\prime)=3(6)x^(6-1)+2(5)x^(5-1) \\ =18x^5+10x^4 \end{gathered}`

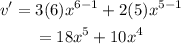
Now put the values in the product rule,

`\begin{gathered} y^(\prime)=(uv)^(\prime) \\ =u^(\prime)v+v^(\prime)u \\ =(12x^2-10x)(3x^6+2x^5)+(18x^5+10x^4)(4x^3-5x^2) \end{gathered}`

Simplifying further,

`\begin{gathered} y^(\prime)=12x^2(3x^6+2x^5)-10x(3x^6+2x^5)+18x^5(4x^3-5x^2)+10x^4(4x^3-5x^2) \\ =36x^8+24x^7-30x^7-20x^6+72x^8-90x^7+40x^7-50x^6 \\ =108x^8-56x^7-70x^6 \end{gathered}`

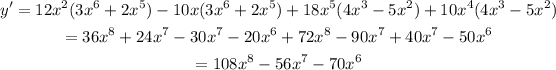
This is the derivative obtained.

From above two methods, we can see the derivative is same in both the cases.