Question

Consider a parabola that intersects the x axis at points (-1,0) and (3,0)

Answer 1

Given that we only have two points known in the parabola, the best way to determine the equation (having the options already) is to substitute the points on each equation to see which one is true for both points:

`\begin{gathered} y=x^2+3x+2 \\ \text{for (-1,0)}\colon \\ 0=(-1)^2+3(-1)+2 \\ \Rightarrow0=1-3+2=3-3=0 \\ \text{for (3,0)}\colon \\ \Rightarrow0=(3)^2+3(3)+2=9+9+2=20 \end{gathered}`

As we can see on the previous example, when we substitute the point (3,0), we get a contradiction, since 0=20 can never happen. Working this way we find that the equation y=x^2-2x-3 yields the desired results:

`\begin{gathered} y=x^2-2x-3 \\ on\text{ (-1,0):} \\ 0=(-1)^2-2(-1)+3=1+2-3=0 \\ on\text{ (3,0):} \\ 0=(3)^2-2(3)-3=9-6-3=9-9=0 \end{gathered}`

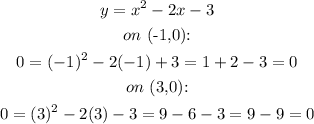
Therefore, the equation of the parabola is y=x^2-2x-3