SOLUTION
(a) The vertex of the parabola
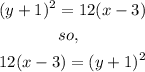
Now,

From the initial equation we have
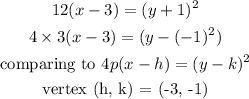
Therefore, the vertex of the parabola is (-3, -1)
(b) The parabola opens at?
Let us see the graph of the parabola
From the image, we can see that the Parabola opens right
(c) The focus
This can be determined using the formula
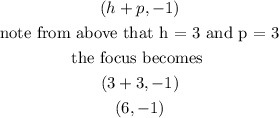
Now, the focus has coordinates (6, -1). Looking at the graph, we can see that from the point x = 6, the focus is 3 units away from the vertex.
(d) The directrix is read from point x = 0.
So, reading from x = 0, from the graph we can see that directrix is 6 units away from thr focus
From our explanation above, we can see that
(e) The focus is the point (6, -1)
(f) And the directrix is
