Question

Which of the following is the graph of f(x)= x² +3x-4?

Answer 1

Given the function

`f(x)=x^2+3x-4`

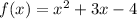
To determine which graph corresponds to this function you have to determine the coordinates of the vertex and the roots of the function.

Vertex

To determine the coordinates of the vertex you have to calculate the x-coordinate using the formula:

`x=-(b)/(2a)`

a is the coefficient of the quadratic term

b is the coefficient of the x-term

The term of the quadratic term, in this case, is a=1 and the term of the x-term is b=3

`\begin{gathered} x=-(3)/(2\cdot1) \\ x=-(3)/(2)=-1.5 \end{gathered}`

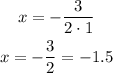
Replace the x-coordinate in the function to calculate the corresponding value of f(x):

`\begin{gathered} f(x)=x^2+6x-4 \\ f(-3)=(-(3)/(2))^2+3\cdot(-(3)/(2))-4 \\ f(-3)=(9)/(4)-(9)/(2)-4 \\ f(-3)=-(25)/(4)=-6.25 \end{gathered}`

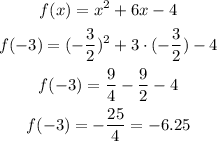
The coordinates of the vertex are (-1.5,-6.25)

Roots of the function

To determine the roots of the function you have to use the quadratic formula:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

a is the coefficient of the quadratic term

b is the coefficient of the x-term

c is the constant of the function

For a=1, b=3, and c=-4

`\begin{gathered} x=\frac{-3\pm\sqrt[]{3^2-4\cdot1\cdot(-4)}}{2\cdot1} \\ x=\frac{-3\pm\sqrt[]{9+16}}{2} \\ x=\frac{-3\pm\sqrt[]{25}}{2} \\ x=(-3\pm5)/(2) \end{gathered}`

Solve the addition and the subtraction separately

Addition

`\begin{gathered} x=(-3+5)/(2) \\ x=(2)/(2) \\ x=1 \end{gathered}`

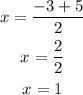
Subtraction

`\begin{gathered} x=(-3-5)/(2) \\ x=(-8)/(2) \\ x=-4 \end{gathered}`

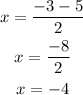
The roots of the function are (1,0) and (-4,0)

The graph that corresponds to this function is