Question

The Lofoten Islands in Norway (one of Mr. Maier's favorite places) has a latitude of 68.4711 ° north of the equator. What is the linear speed as the earth rotates at that latitude? Use 3961.3 miles for the radius of the earth.

Answer 1

`v=wr`
`w=(2\pi)/(T)`

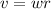
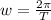
The equations are the linear velocity and angular moment respectively.

Since we have that the rotation of the Earth takes 24 hours, we transform it into seconds, that is:

`24\cdot60\cdot60=86400`

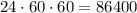
So, it has a period of 86400 seconds.

We now, transform the radius to the IS (from miles to meters), that is:

And, since the latitude is 68.4711° we solve in the function given at the start, that is:

`w=(2\pi)/(86400)\Rightarrow w=7.272205217\cdot10^5`

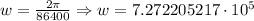
Then we divide this value by the time it takes to do a revolution of the Earth, the previously calculated 86400 seconds, that is:

`v=wr\Rightarrow w=(7.272205217\cdot10^(-5))(6375.1)`
`\Rightarrow v\approx0.464`

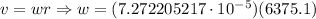
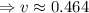
So, the linear velocity at that latitude is approximately 0.464 Km/s.