Question:
Solution:
The population growth is given by the following equation:
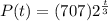
where P represents the number of individuals and t represents the number of years from the time of introduction. Now, if we have a population of 5656 fish, then the above equation becomes:
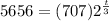
this is equivalent to:
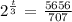
this is equivalent to:
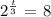
this is equivalent to:
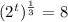
now, the inverse function of the root function is the exponential function. So that, we can apply the exponential function to the previous equation:
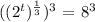
this is equivalent to:
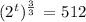
this is equivalent to:
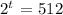
now, we can apply the properties of the logarithms to the previous equation:
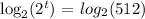
this is equivalent to:
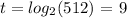
we can conclude that the correct answer is:
9 years