Question

Solve the system of equations. If the system has no solution, say that it is inconsistent.

Answer 1

D. The system is inconsistent

Explanation:

Given the below system of equations;

`\begin{gathered} 2x-2y+5z=11\ldots\ldots\ldots\text{Equation 1} \\ 6x-5y+13z=30\ldots\ldots\ldots\text{.}\mathrm{}\text{Equation 2} \\ -2x+3y-7z=-13\ldots\ldots\ldots\text{Equation 3} \end{gathered}`

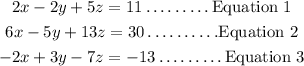
We'll follow the below steps to solve the above system of equations;

Step 1: Add Equation 1 and Equation 3;

`\begin{gathered} (2x-2x)+(-2y+3y)+(5z-7z)=(11-13) \\ y-2z=-2 \\ y=2z-2\ldots\ldots\text{.}\mathrm{}\text{Equation 4} \end{gathered}`

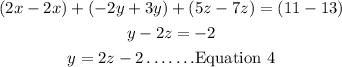
Step 2: Multiply Equation 3 by 3, we'll have;

`-6x+9y-21z=-39\ldots\ldots\text{.Equation 5}`

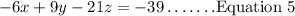
Step 3: Add Equation 2 and Equation 5, we'll have;

`4y-8z=-9\ldots\ldots\ldots\text{Equation 6}`

Step 4: Put Equation 4 into Equation 6 and solve for z;

`\begin{gathered} 4(2z-2)-8z=-9 \\ 8z-8-8z=-9 \\ 8z-8z=-9+8 \\ 0=-1 \end{gathered}`

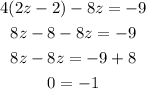
From the above, we can see that we do not have a solution for z, therefore, we can say that the system of equations has no solution, hence, it is inconsistent.