Question

Which of the following is the equation c^(4d+1)=7a-b written in logarithmic form?

Answer 1

We have the expression:

`c^((4d+1))=7a-b`

We can apply logarithm to both sides. We would use it in order to get "4d+1". Then, we would apply logarithm with base c. This is beacuse of the definition of logarithm:

`\log _c(x)=y\Leftrightarrow c^y=x`

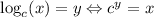
If we apply this to our expression, we get:

`\begin{gathered} c^((4d+1))=7a-b \\ \log _c(c^((4d+1)))=\log _c(7a-b) \\ 4d+1=\log _c(7a-b) \end{gathered}`

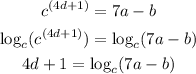
If we rearrange both sides, we get the expression in Option B (we have to switch the sides):

`\begin{gathered} 4d+1=\log _c(7a-b) \\ \log _c(7a-b)=4d+1 \end{gathered}`

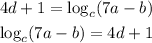
Answer: Option B