Question

Change the quadratic equation from standard from to vertex form

Answer 1

`y=\left[x-\left(-2\right)\right]^2+\left(-9\right)`

Step-by-step explanation:

Given the quadratic equation in standard form:

`y=x^2+4x-5`

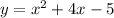
1. Transpose the c-value to the left side of the equation.

`y+5=x^2+4x`

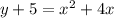
2. Complete the square of the expression on the right side of the equation to get a perfect square trinomial. Add the resulting term to both sides.

`\begin{gathered} y+5+((4)/(2))^2=x^2+4x+((4)/(2))^2 \\ \implies y+5+(2)^2=x^2+4x+(2)^2 \end{gathered}`

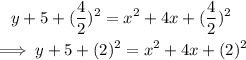
3. Add the numbers on the left and factor the trinomial on the right.

`$ y+9=(x+2)^2 $`

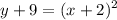
4. Transpose the number across to the right side to get the equation into the vertex form, y=a(x-h)²+k.

`y=(x+2)^2-9`

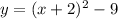
5. Make sure the addition and subtraction signs are correct to give the proper vertex form.

`y=\left[x-\left(-2\right)\right]^2+\left(-9\right)`

The vertex form of the given quadratic equation is:

`y=\left[x-\left(-2\right)\right]^2+\left(-9\right)`