Question

The note A has a frequency of 1,760 hertz. The note D has a period of 1,175 hertz. Find theratio of A to D to two decimal places. Express the answer in integer ratio form.

Answer 1

The speed of the musical note A is found by multiplying its frequency (440 Hz) by its wavelength (0.784 m), resulting in approximately 344.96 m/s.

Step-by-step explanation:

To calculate the speed of the musical note A, you can use the formula for wave speed, which is the product of frequency (f) and wavelength (λ). Given the frequency of 440 Hz for the musical note A and its wavelength of 0.784 m, the speed (v) can be calculated as follows:

v = f × λ

v = 440 Hz × 0.784 m

v = 344.96 m/s

Therefore, the speed of the musical note A is approximately 344.96 meters per second.

Answer 2

Ratios

Note A has a frequency of

fa=1,760 Hz

Note D has a period of 1,175 hertz

(the previous data should be frequency, not period)

We are required to find the ratio of A to D. Let's call it r:

`r=(1,760^(\prime))/(1,175)`

Dividing: r = 1.4978. Rounding to two decimal places:

r = 1.50

Now to express the answer in integer ratio form, we need to simplify the fraction.

First, we divide by 5 up and down:

`r=(352^(\prime))/(235)`

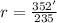
There are no more common divisors for both numbers, thus the integer ratio form is r = 352/235