Question

Use the values of the vertex and point to write the equation of the graph in standard form

Answer 1

Step-by-step explanation

The vertex form of a quadratic function is:

`\begin{gathered} y=a(x-h)^2+k \\ \text{ Where} \\ (h,k)\text{ is the vertex of the parabola } \end{gathered}`

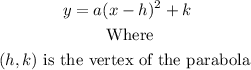
The standard form of a quadratic function is:

`y=ax^2+bx+c`

We can do the following steps to solve the exercise.

Step 1: We replace the values of h,k, x, and y into the vertex form of a quadratic equation, and we solve for a.

`\begin{gathered} h=1 \\ k=-5 \\ x=3 \\ y=-1 \end{gathered}`
`\begin{gathered} y=a(x-h)^(2)+k \\ -1=a(3-1)^2-5 \\ -1=a(2)^2-5 \\ -1=4a-5 \\ \text{ Add 5 from both sides} \\ -1+5=4a-5+5 \\ 4=4a \\ \text{ Divide by 4 from both sides} \\ (4)/(4)=(4a)/(4) \\ 1=a \end{gathered}`

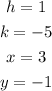
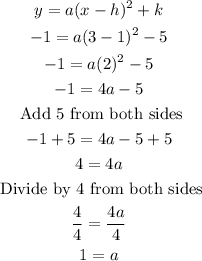
Step 2: We replace the values of a,h, and k into the vertex form of a quadratic equation.

`\begin{gathered} y=a(x-h)^(2)+k \\ y=1(x-1)^2-5 \end{gathered}`

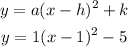
Step 3: We expand the expression inside the parentheses and combine like terms to convert the function into its standard form.

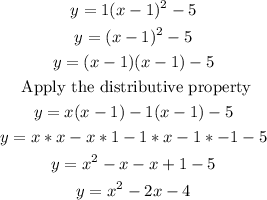
`\begin{gathered} y=1(x-1)^(2)-5 \\ y=(x-1)^2-5 \\ y=(x-1)(x-1)-5 \\ \text{ Apply the distributive property} \\ y=x(x-1)-1(x-1)-5 \\ y=x*x-x*1-1*x-1*-1-5 \\ y=x^2-x-x+1-5 \\ y=x^2-2x-4 \end{gathered}`Answer

The equation of the graph in standard form is:

`y=x^(2)-2x-4`