Type the correct answer in the box. Rewrite the quadratic function in the form that best reveals the zeros of the function.

Question

asked Jan 21, 2023 205k views

1 Answer

Kshatriiya · Answer 1 · 2023-01-25T13:11:44+0000

Answer:

f(x) = (2x + 3)(2x + 1)

Step-by-step explanation:

The form that best reveals the zeros of the function is:

f(x) = (x - a)(x - b)

Where a and b are the zeros of the function.

So, we need to apply the distributive property as:

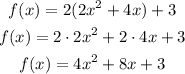
$\begin{gathered} f(x)=2(2x^2+4x)+3 \\ f(x)=2\cdot2x^2+2\cdot4x+3 \\ f(x)=4x^2+8x+3 \end{gathered}$

Then, we can factorize the quadratic function as:

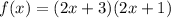
So, now we can identify the zeros of the function if we solve the following equation:

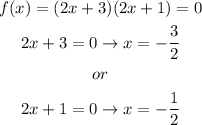
$\begin{gathered} f(x)=(2x+3)(2x+1)=0 \\ 2x+3=0\rightarrow x=-(3)/(2) \\ or \\ 2x+1=0\rightarrow x=-(1)/(2) \end{gathered}$

Therefore, the form that best reveals the zeros in the function is:

f(x) = (2x + 3)(2x + 1)