Question

Find the length of arc FH. Round to the nearest hundredth.(Degrees)

Answer 1

Given the circle G

As shown, m∠FGH = 36

And the radius of the circle = r = FG = 10 units

we will find the length of the arc FH using the formula:

`\text{Arc}=\theta\cdot r`

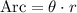
The given angle measured in degree, we will convert it to radian

So,

`\theta=36\cdot(\pi)/(180)=(\pi)/(5)`

So, the length of the arc =

`(\pi)/(5)\cdot10=2\pi\approx6.283185`

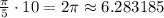
Round to the nearest hundredth.

So, the answer will be the length of the arc FH = 6.28