Question

Triangle OPQ is similar to triangle RST. find the neasure of side ST. Round to the nearest tenth if necessary

Answer 1

By definition, when two figures are similar, their corresponding angles are congruent (this means that they have equal measure) and the ratios of the lengths of their corresponding sides are the same.

In this case you know that the triangles shown in the picture are similar, therefore, you can set up the following proportion:

`(OP)/(RS)=(PQ)/(ST)`

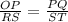
You can identify that:

`\begin{gathered} OP=37 \\ RS=7 \\ PQ=48 \end{gathered}`

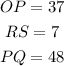
Therefore, you can substitute values into the proportion:

`(37)/(7)=(48)/(ST)`

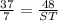
Now you have to solve for ST:

`\begin{gathered} (ST)((37)/(7))=48 \\ \\ ST=(48)((7)/(37)) \\ \\ ST\approx9.1 \end{gathered}`

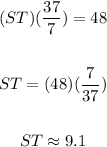
The answer is:

`ST\approx9.1`