Question

Given the polynomial P(x)= x^3 + 10x^2 + 25xa. List all of the potential rational roots b. Find and list all the actual roots of P(x), and the multiplicity of each root

Answer 1

a)

In order to find the list of all potential rational roots, let's find the factors of the division between the constant term and the leading term.

Since the constant term is zero, so the only potential rational root in the list is 0.

b)

Since the constant term is zero, so 0 is a root of the polynomial. Then, let's factor it to find the remaining roots:

`\begin{gathered} x^3+10x^2+25x=0 \\ x(x^2+10x+25)=0 \\ x^2+10x+25=0 \end{gathered}`

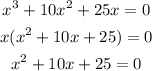
Solving this quadratic equation using the quadratic formula, we have:

`\begin{gathered} ax^2+bx+c=0 \\ x^2+10x+25=0 \\ a=1,b=10,c=25 \\ \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x_1=\frac{-10+\sqrt[]{100-100}}{2}=(-10+0)/(2)=-5 \\ x_2=(-10-0)/(2)=-5 \end{gathered}`

Therefore the actual roots of P(x) are:

0 (multiplicity 1) and -5 (multiplicity 2).