Question

A larger pipe fills a water tank twice as fast as a smaller pipe. When both pipes are used, they fill the tank in 55 hours. If the larger pipe is left off, then how long would it take the smaller pipe to fill the tank?

Answer 1

For this exercise you need to use the Work-rate formula. This is:

`(t)/(t_A)+(t)/(t_B)=1`

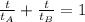
Where:

- "t" is the time for the objects A and B together.

- The individual time for object A is:

`t_A`

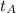
- The individual time for object B is:

`t_B`

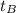
In this case, you can idenfity that:

`\begin{gathered} t=55 \\ t_A=2t_B \\ _{} \end{gathered}`

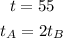
Substitute them into the formula:

`\frac{55}{2t_B_{}_{}}+(55)/(t_B)=1`

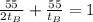
Now you must solve for:

`t_B`

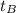
You get that this is:

`\begin{gathered} (55+2(55))/(2t_B)=1 \\ \\ (55+110)/(2t_B)=1 \\ 165=(1)(2t_B) \\ \\ (165)/(2)=t_B_{} \\ \\ t_B=82.5 \end{gathered}`

The answer is: It takes the smaller pipe 82.5 hours to fill the tank.