Question

Express the distance,d, from a point on the graph x+y=2 to the point (6,8) as a function of x

Answer 1

`d=\sqrt[]{2(x^2+36^{})}`

Step-by-step explanation:

Given the equation of the line as;

`x+y=2`

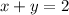
We can express y in terms of x by subtracting x from both sides of the equation;

`y=-x+2`

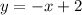
Let the point on the line be P(x, y)

We'll use the below distance formula to determine the distance between point P(x, y) to the given point (6, 8) as seen below;

`d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`
`\begin{gathered} d=\sqrt[]{(6-x)^2+(8-y)^2} \\ d=\sqrt[]{(36-12x+x^2)+\lbrack8-(-x+2)\rbrack^2} \\ d=\sqrt[]{(36-12x+x^2)+(6+x)^2} \end{gathered}`
`\begin{gathered} d=\sqrt[]{(36-12x+x^2)+(36+12x+x^2)} \\ d=\sqrt[]{72+2x^2} \\ d=\sqrt[]{2(x^2+36^{})} \end{gathered}`