Question

The 5 participants in a 200-meter dash had the following finishing times in seconds)24, 28, 26, 30, 32Send data to calculatorAssuming that these times constitute an entire population, find the standard deviation of the population. Round your answer to two decimal places,

Answer 1

Given:

Data x: 24, 28, 26, 30, 32

n = 5

Asked: What is the standard deviation of the population?

Formula:

`\text{standard deviation = }\sqrt[]{\frac{\sum ^{}_{}(x-\bar{x})^2}{n}}`

Solution:

Step 1: We will get the average of the data given.

NOTE: Bar x is also the mean or the average.

`\begin{gathered} \bar{x}\text{ = }(24+28+26+30+32)/(5)\text{ } \\ \bar{x}=\text{ 28} \end{gathered}`

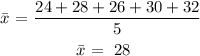
Step 2: We will subtract the mean from each number.

Step 3: We will square the differences and get the summation.

Step 4: We will substitute the acquired values to find the standard deviation using the formula above.

`\begin{gathered} \text{standard deviation = }\sqrt[]{\frac{\sum ^{}_{}(x-\bar{x})^2}{n}} \\ \text{standard deviation = }\sqrt[]{\frac{40^{}}{5}}\text{ } \\ \text{standard deviation = 2}\sqrt[]{2}\text{ = }2.828427125 \end{gathered}`

ANSWER: standard deviation = 2.83 (Rounded off to 2 decimal places)