Question

Using the Quotient Rule, use the Quotient Rule to find the derivative of the function.

Answer 1

To find the derivative of
`f(x) = (x^2)/(2√(x) + 1)` using the Quotient Rule, calculate the derivatives of the numerator and the denominator separately, then apply the rule to obtain the derivative of the function.

Step-by-step explanation:

Using the Quotient Rule to find the derivative of the function
`f(x) = (x^2)/(2√(x) + 1)`, we need to define the numerator as
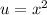`u = x^2` and the denominator as
`v = 2√(x) + 1`. The Quotient Rule states that the derivative of a function in the form of u/v is given by
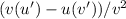`(v(u') - u(v')) / v^2`. So, calculate the derivatives u' = 2x and
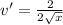`v' = (2)/(2√(x))` (using the chain rule and power rule for v'). Substituting these into the Quotient Rule formula gives the derivative of the function.

Firstly,

u' = 2x

Secondly,
`v' = 1/√(x)`

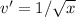
Thus, the derivative of f(x) becomes:

`f'(x) = ((2√(x) + 1)(2x) - (x^2)(1/√(x)))/((2√(x) + 1)^2)`. This simplifies to give the final expression for the derivative after combining like terms and simplifying the fraction.

Answer 2

In calculus, the quotient rule is a method of finding the derivative of a function that is the ratio of two differentiable functions. This rule is given by the following expression:

`((f)/(g))^(\prime)=(f^(\prime)g-fg^(\prime))/(g^2)`

Applying this rule in our problem, we have:

`\begin{gathered} f^(\prime)(x)=((x^2)^(\prime)(2√(x)+1)-(x^2)(2√(x)+1)^(\prime))/((2√(x)+1)^2) \\ \\ =((2x)(2√(x)+1)-(x^2)(2\cdot(1)/(2)(1)/(√(x))))/(4x+4√(x)+1) \\ \\ =(4x√(x)+2x-x√(x))/(4x+4√(x)+1) \\ \\ =(3x√(x)+2x)/(4x+4√(x)+1) \end{gathered}`