Solve: cot^2((pix)/2)=3

Question

asked Apr 10, 2023 106k views

1 Answer

Hydrargyrum · Answer 1 · 2023-04-17T18:19:23+0000

We are given the following equation:

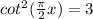
$cot^2((\pi)/(2)x)=3$

To solve for "x" we will take the square root to both sides:

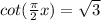
$cot((\pi)/(2)x)=√(3)$

Now, we take the inverse function of cotangent:

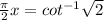
$(\pi)/(2)x=cot^(-1)√(2)$

Solving the operations:

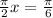
$(\pi)/(2)x=(\pi)/(6)$

Now, we can cancel out the pi:

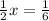
Now, we multiply both sides by 2:

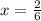
Simplifying:

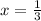
Therefore, the value of "x" is 1/3