Question

The sum of the speeds of two trains is 721.4 miles per hour. If the speed of the first train is 4.6 mph faster than the second train, find the speeds of each

Answer 1

Given:

The sum of the speeds of two trains is 721.4

Let the speed of the trains are x and y

So,

`x+y=721.4\rightarrow(1)`

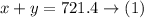
And the speed of the first train is 4.6 mph faster than the second train

So,

`x-y=4.6\rightarrow(2)`

Solve the equations (1) and (2) to find x and y

Add the equations to eliminate (y) then solve for (x):

`\begin{gathered} 2x=721.4+4.6 \\ 2x=726 \\ x=(726)/(2)=363 \end{gathered}`

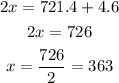
Substitute (x) into the first equation then solve for (y):

`\begin{gathered} 363+y=721.4 \\ y=721.4-363=358.4 \end{gathered}`

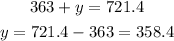
So, the answer will be:

The speeds of the trains are 363 mph and 358.4 mph