Question

The following infinite geometric series will have a finite sum:1/81 - 1/27 + 1/9 -1/3 + ....TrueFalse

Answer 1

Step 1: Determine if if the infinite geometric series is divergence or convergence

If the common ratio is greater than or equals 1, then it is divergence but if r is less than 1, it is convergence.

`\begin{gathered} \text{divergence if }\lvert r\rvert\ge1 \\ \text{convergence if }\lvert r\rvert<1 \end{gathered}`

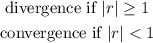
Step 2: Find common ratio r

`\begin{gathered} r=(a_2)/(a_1)=(a_3)/(a_2)_{} \\ r=-(1)/(27)*(81)/(1)=-(81)/(27)=-(4)/(3) \end{gathered}`
`\lvert r\rvert=\lvert-(4)/(3)\rvert=(4)/(3)`

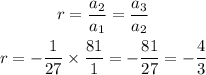
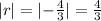
From the value of the absolute value of r gotten, it can be observed that r is greater than 1 or equals 1, hence it is divergence.

Hence, the series will have an infinitely large sum. The correct option is FALSE