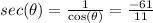Question

Suppose that is an angle in standard position whose terminal side intersects the unit circle at1160616169)Find the exact values of sin 0, seco, and tan 0.

Answer 1

So, here we have the point:

`(-(11)/(61),(60)/(61))`

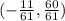
This is situated at the quadrant II.

Remember that sin(a) is a relation between the opposite side of the angle a and the hypotenuse of the triangle.

To find the hypotenuse, we apply the Pythagorean Theorem:

`\begin{gathered} h=\sqrt[]{((60)/(61))^2+((-11)/(61))^2} \\ h=1 \end{gathered}`

Notice that as this point is in the unit circle, the hypotenuse is 1.

Now,

`\sin (\theta)=(60)/(61)`

And,

`sec(\theta)=(1)/(\cos (\theta))=(-61)/(11)`
`\text{tan(}\theta)=((60)/(61))/((-11)/(61))=(-60)/(11)`