The perimeter of the rectangular plot of land is given by the expression below
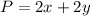
On the other hand, since the available money to buy fence is D dollars,
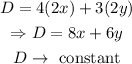
Furthermore, the area of the enclosed land is given by

Solving the second equation for x,

Substituting into the equation for the area,
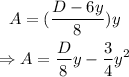
To find the maximum possible area, solve A'(y)=0, as shown below
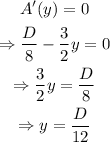
Therefore, the corresponding value of x is
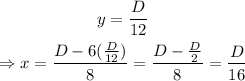
Thus, the dimensions of the fence that maximize the area are x=D/16 and y=D/12.
As for the used money,
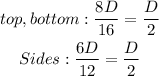
Half the money was used for the top and the bottom, while the other half was used for the sides.