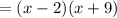Question

I'm not understanding 9th grade math right now what we are currently learning is finding Solutions of quadratic equations by factoring, could you help me?

Answer 1

EXPLANATION

Given the equation:

`x^2\text{ + 7x -18 = 0}`

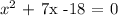
We can apply the quadratic equations formula as shown as follows:

Break the expression into groups:

For:

`ax^2+bx+c`

Find u,v such that u*v = a*c and u+v = b and group into (ax^2+ux)+(vx+c)

a=1, b=7, c=-18

u*v=-18, u+v = 7

Find the primer factors of 18:

18 / 2 = 9

9 / 3 = 3

2,3 are all prime numbers, therefore no further factorization is possible.

Multiply the prime factors of 18: 6,9

Add the prime factors: 2,3

Add 1 and the number 18 itself

1, 18

The factors of 18:

1, 2, 3 , 6, 9, 18

Negative factors of 18:

Multiply the factors by -1 to get the negative factors:

-1, -2, -3, -6, -9, -18

For every two factors such that u*v=-18 , check if u+v = 7:

`\mathrm{Check}\: u=1,\: v=-18\colon\quad \: u\cdot v=-18,\: u+v=-17\quad \Rightarrow\quad \mathrm{False}`
`\mathrm{Check}\: u=2,\: v=-9\colon\quad \: u\cdot v=-18,\: u+v=-7\quad \Rightarrow\quad \mathrm{False}`
`\mathrm{Check}\: u=3,\: v=-6\colon\quad \: u\cdot v=-18,\: u+v=-3\quad \Rightarrow\quad \mathrm{False}`
`\mathrm{Check}\: u=6,\: v=-3\colon\quad \: u\cdot v=-18,\: u+v=3\quad \Rightarrow\quad \mathrm{False}`
`\mathrm{Check}\: u=9,\: v=-2\colon\quad \: u\cdot v=-18,\: u+v=7\quad \Rightarrow\quad \mathrm{True}`
`\mathrm{Check}\: u=18,\: v=-1\colon\quad \: u\cdot v=-18,\: u+v=17\quad \Rightarrow\quad \mathrm{False}`

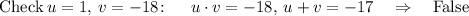
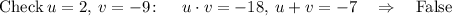
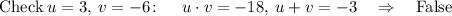
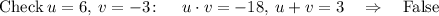
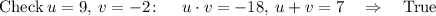
u=9, v=-2

Group into:

`(ax^2+ux)+(vx+c)`
`(x^2-2x)+(9x-18)`

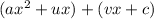
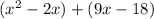
Factor out x from x^2 -2x

x^2 -2x

Factor out common term x:

=x(x-2)

Factor out 9 from 9x - 18:

Rewrite 18 as 2*9:

9x - 9*2

Factor out common term 9:

9(x-2)

=x(x-2) + 9(x-2)

Factor out common term x-2:

`=\mleft(x-2\mright)\mleft(x+9\mright)`

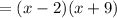
The solution to the quadratic equation x^2 + 7x - 18 = 0 applying the factorizing method is:

`=(x-2)(x+9)`