Question

1. At what rate must money be invested to double the money over a 10-year time frame?

Answer 1

For this problem, we want to assume the interest rate is compounded annually.

We are given the time frame (n) for the investment to be 10 years.

Let the initial amount be P.

After 10 years, the amount should be double implying it should be 2P.

Let the rate at which the money must be invested be r.

Using the compound interest formula:

`A\text{ = P(1 + }(r)/(100))^n`

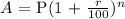
Where;

A is the amount

P is the principal

r is the rate

and n is the number of years.

Substituting, we have:

`2P\text{ = P(1 + }(r)/(100))^(10)`

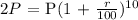
Divide both sides by P

`\begin{gathered} (2P)/(P)\text{ = }\frac{P(1\text{ + }(r)/(100))^(10)}{P} \\ (1\text{ + }(r)/(100))^(10)\text{ = 2} \end{gathered}`

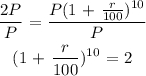
Taking the logarithm of both sides and simplifying further, we have: