Question

Find three consecutive odd integers such that the square of the first increased the product of the other two is 28.

Answer 1

Since these numbers are odds, they are of the form:

`2x+1`

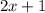
Let's take this as the first.

The second one must be:

`2x+3`

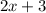
And the last one:

`2x+5`

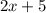
The square of the first one increased the product of the other two is 28:

`(2x+1)^2+(2x+3)(2x+5)=28`

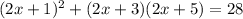
If we take k=2x+1, we get:

`k^2+(k+2)(k+4)=28`
`k^2+k^2+6k+8=28`
`2k^2+6k+8=28`
`2k^2+6k+8-28=0`
`2k^2+6k-20=0`
`k^2+3k-10=0`
`(k+5)(k-2)=0`

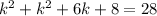
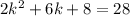
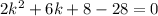
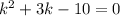
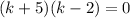
K could be -5 or 2, but because has to be a odd number k=-5.

Lets check:

`(-5)^2+(-3)(-1)`
`25+3`
`28`

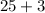
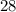
The consecutive odd numbers are -5 , -3 and -1