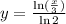Solution:
Using the exponential function below
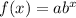
Where

For exponential decay,
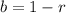
For exponential growth
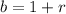
Suppose, we are given a function
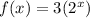
The function above will have an inverse.
To find the inverse of the function, where f(x) = y,
Firstly, replace x with y and y with x as shown below
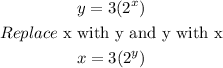
Then, solve for y

Hence, the inverse is