Question

The Height in feet above the ground of an arrow after it is shot can be molded  by Y= -16 X squared +63+4. Can the arrow pass over a tree that is 68 feet tall?

Answer 1

From

`\begin{gathered} y=-16x^2+63x+4 \\ At\text{ maxi}mum\text{ height }\frac{d\text{ y}}{d\text{ x}}\text{ is = 0} \\ So\text{ we will differentiate }y=-16x^2+63x+4 \\ y=-16x^2+63x+4 \\ \frac{d\text{ y}}{d\text{ x}}\text{ = -32x + 63 = 0} \\ -32x\text{ + 63 = 0} \\ 32x\text{ = 63} \\ \text{x = }(63)/(32)\text{ = 1.97} \end{gathered}`

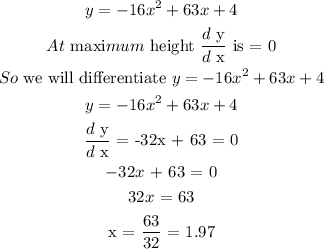
Now, we will substitute 1.97 for x into y

`\begin{gathered} \text{From } \\ y=-16x^2+63x+4 \\ y=-16(1.97)^2+63(1.97)+4 \\ y\text{ = -62.09 + 124.11 + 4} \\ y\text{ = 66.02 } \end{gathered}`

Since y which is the height of the arrow is 66.02 feet, and the tree is 68 feet tall, the arrow can not pass over the tree. Because for the arrow to pass over the tree, its height must be above 68 feet tall.