Question

A cone and a cylinder have equal radii, r, and equal altitudes, h. If the slant height of the cone is l, then the ratio of the lateral area of the cone to the lateral area of the cylinder isA. l:2hB. l:2rC. 2l:hD. l:h

Answer 1

Given -

A cone and a cylinder have equal radii = r,

and equal altitudes = h

The slant height of the cone = l

To Find -

The ratio of the lateral area of the cone to the lateral area of the cylinder =?

Step-by-Step Explanation -

The lateral surface area of the cylinder = 2πrh

The lateral surface area of the cone = πrl

So,

The ratio of the lateral area of the cone to the lateral area of the cylinder =

`\begin{gathered} \frac{The\text{ }lateral\text{ }surface\text{ }area\text{ }of\text{ }the\text{ }cone}{The\text{ }lateral\text{ }surface\text{ }area\text{ }of\text{ }the\text{ }cylinder}\text{ = }(\pi rl)/(2\pi rh) \\ \\ =\text{ }(l)/(2h) \end{gathered}`

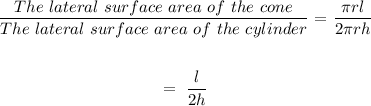
Final Answer -

The ratio of the lateral area of the cone to the lateral area of the cylinder =

A. l:2h