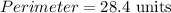Question

The points D(4,−5)(4,−5), E(4,0)(4,0), F(−5,2)(−5,2), and G(−5,−3)(−5,−3) form parallelogram DEFG. Plot the points then click the "Graph Quadrilateral" button. Then find the perimeter of the parallelogram. Round your answer to the nearest tenth if necessary.

Answer 1

The coordinates of the parallelogram are given to be:

`\begin{gathered} D=\left(4,-5\right) \\ E=\left(4,0\right) \\ F=\left(-5,2\right) \\ G=\left(-5,-3\right) \end{gathered}`

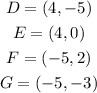
The graph is shown below:

To get the perimeter of the shape, the lengths of the lines are to be calculated.

According to the property of a parallelogram, the opposite sides are equal. Therefore:

`\begin{gathered} EF=DG \\ FG=ED \end{gathered}`

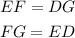
The length of line ED can be calculated to be:

`ED=0-(-5)=5\text{ units}`

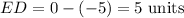
The length of line EF can be calculated using the distance formula:

`\begin{gathered} EF=√((x_2-x_1)^2+(y_2-y_1)^2) \\ \therefore \\ EF=√((-5-4)^2+(2-0)^2) \\ EF=√(81+4) \\ EF=√(85) \end{gathered}`

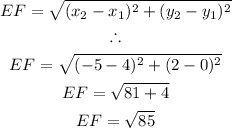
Therefore, the perimeter is calculated as follows:

`Perimeter=2(5)+2(√(85))=28.4`

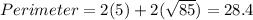
ANSWER

`Perimeter=28.4\text{ units}`