Question

find the distance from point A(15,-21) to the line 5x + 2y = 4 . round your answer to the nearest tenth

Answer 1

We will find the distance from point A to the line as follows:

*First: We solve for 0 on the equation of the line, that is:

`5x+2y=4\Rightarrow5x+2y-4=0`

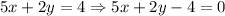
Now, we can see that the equation of the line has the form:

`Ax+Bx+C=0`

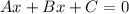
So, we use the following expression to determine the distance from the point to the line:

`d=\fracAx_1+By_1+C{\sqrt[]{A^2+B^2}}`

Now, we replace the values and solve for d:

`d=\frac(5)(15)+(4)(-21)+(-4){\sqrt[]{5^2+2^2}}\Rightarrow d=\frac-13{\sqrt[]{29}}`
`\Rightarrow d=\frac{13}{\sqrt[]{29}}\Rightarrow d\approx2.4`

So, the distance from point (15, -21) to the line 5x + 2y = 4 is approximately 2.4 units.