Question

In a certain year congress begin debating a new healthcare bill a poll of 1000 Americans at the time indicated that 449 oppose the bill 293 favorite the bill and 258 we’re not sure based on these results assume you asked randomly selected Americans to question express your answer as exact decimals

Answer 1

Given:

`\begin{gathered} Opposed\text{ \lparen American\rparen}=449 \\ Favoured\text{ \lparen American\rparen}=293 \\ Not\text{ }sure\text{ \lparen American\rparen}=258 \\ Total=1000 \end{gathered}`

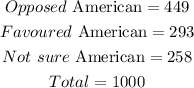
To Determine: The probability of a randomly selected American was in favor

Solution

The probability of an event A is the ratio of the number of element in A to the total number of element in the sample space

`\begin{gathered} P(A)=(n(A))/(n(S)) \\ P(A)=Probability\text{ of event A} \\ n(A)=number\text{ of elements in A} \\ n(S)=number\text{ of elements in the sample space} \end{gathered}`

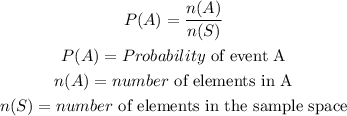
Apply the probability formula to solve for the probability of an event A is the ratio of the number of element in A to the total number of element in the sample space

Therefore,

`\begin{gathered} P(F)=\frac{number\text{ of Americans in favor}}{total\text{ number of Americans}} \\ P(F)=Probability\text{ of American in favor} \\ P(F)=(293)/(1000) \\ P(F)=0.293 \end{gathered}`

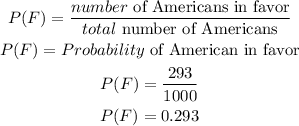
Hence, the probability of a randomly selected American was in favor is 0.293