Tennsion 1= horizontal = 484.94 N
Tension 2 = slanted string = 560 N
Step-by-step explanation
Step 1
Free body diagram
Newton's first law says that if the net force on an object is zero, like in this case the mass is in rest,then that object will have zero acceleration
so
Step 1
set the equations:
a) for x-axis
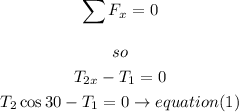
b) for y -axis
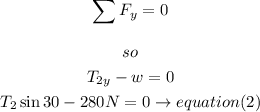
Step 2
Solve the equations
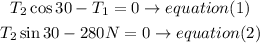
a) solve for T2in equation (2)
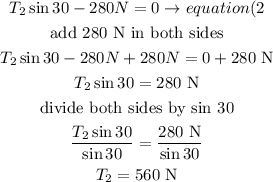
b) replace the T2 value in equation (1) to find T1
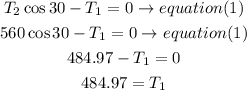
therefore
Tennsion 1= horizontal = 484.94 N
Tension 2 = slanted string = 560 N
I hope this helps you