We are given that the height of a ball is given by the following equation:
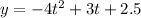
To determine the time it takes the ball to hit the ground we must set the equation to zero, like this:
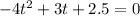
Now, we will multiply both sides by -1:
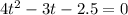
Now, to determine the values of "t" we use the fact that the equation has the following form:
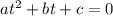
Therefore, its solution is given by the quadratic formula:
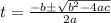
Now, we substitute the values:
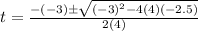
Now, we solve the operations inside the radical:

Solving the radical:
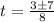
Now, we take the positive value because we want the time to have a positive value:
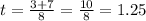
Therefore, it takes the ball 1.25 seconds to reach the ground.