Let W = the three sides to make the width of the two corrals
Let L = the one side parallel to the river.
Area
A = L * W
Replace L with (300-3W)
A = (300-3W) * W
A = -3W^2 + 300W
A quadratic equation, the axis of symmetry will be the value for max area
Find that using x = -b/(2a)
In this equations: x = W; a = -3; b = 300
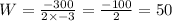
W = +50 yd is the width for max area.
Find the max area, substitute 50 for W in the area equation:
A = -3(50^2) + 300(50)
A = -3(2500) + 15000
A = -7500 + 15000
A = 7500 sq/yds is max area
Hence the largest total area that can be enclosed is 7500 sq. yd.