Answer:
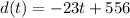
Explanation:
Assuming the hurricane continues on the same path at the same speed means the relationship between speed and time will be linear. This means our function can be written in slope-intercept form,
 . For our function, it will be written as
. For our function, it will be written as
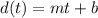 , where t is time, d is distance, m is the slope of the line, and b is the y-intercept. We can solve for slope by using the formula
, where t is time, d is distance, m is the slope of the line, and b is the y-intercept. We can solve for slope by using the formula
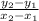 , where x2 and x1 are the times 8 and 3, respectively, and y2 and y1 are the distances 372 and 487, respectively. This gives us a slope of -23.
, where x2 and x1 are the times 8 and 3, respectively, and y2 and y1 are the distances 372 and 487, respectively. This gives us a slope of -23.
We can solve for b by inputting the values we've been given and using algebra.
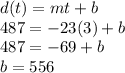
This gives us the equation
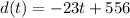
Something to note, since we let 3:00 pm and 8:00 pm be the values x=3 and x=8, 12:00 pm would be x=0, and values in the morning would be negative, like 9:00 am would be x=-3.