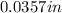Question

To keep Paul Senior from blowing a gasket, Paul Junior must deviate from the ideal area of the disk, which is 1000 in2, by less than ±4 in2. How close to the ideal radius must the Flowjet (the machine that cuts the disk) be to maintain tranquility at OCC? Use 3 significant figures to report your answer.

Answer 1

The area of a circle with radius r is given by the formula:

`A=\pi r^2`

If we change the value of r by a small amount Δr, the new value of the area will be:

`\begin{gathered} A+\Delta A=\pi(r+\Delta r)^2 \\ =\pi(r^2+2r\Delta r+\Delta r^2) \end{gathered}`

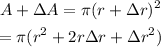
We can neglect the term Δr^2 since we are assuming that Δr is a very small quantity. Then:

`A+\Delta A=\pi r^2+2\pi r\Delta r`

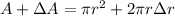
Substitute A=πr^2 and isolate Δr from the equation:

`\begin{gathered} \Rightarrow\pi r^2+\Delta A=\pi r^2+2\pi r\Delta r \\ \Rightarrow\Delta A=2\pi r\Delta r \\ \Rightarrow\Delta r=(\Delta A)/(2\pi r) \end{gathered}`

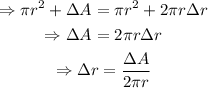
Assuming that the ideal area of the disk is 1000in^2, calculate the ideal radius of the disk:

`\begin{gathered} A=\pi r^2 \\ \Rightarrow r^2=(A)/(\pi) \\ \Rightarrow r=\sqrt[]{(A)/(\pi)} \\ \Rightarrow r=\sqrt[]{(1000in^2)/(\pi)} \\ \Rightarrow r=17.84124116\ldots in \end{gathered}`

Substitute the value of r as well as the variation on the value of the area ΔA=4in^2 to find the variation in the value of the radius:

`\begin{gathered} \Delta r=(4in^2)/(2\pi(17.84124116\ldots in)) \\ =0.03568248232\ldots in \end{gathered}`

Up to 3 significant figures, the variation in the value of the radius must be less than:

`0.0357in`