Find the approximate area of the shaded region below, consisting of a right triangle with a circle cut out of it. Use as an approximation for

Question

asked Oct 11, 2023 141k views

1 Answer

Penanghill · Answer 1 · 2023-10-16T09:33:51+0000

Consider that the area of a triangle with base (b) and height (h) is given by,

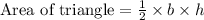
$\text{Area of triangle}=(1)/(2)* b* h$

According to the given problem,

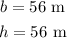
$\begin{gathered} b=56\text{ m} \\ h=56\text{ m} \end{gathered}$

So the area of the triangle becomes,

$\begin{gathered} A_T=(1)/(2)*56*56 \\ A_T=1568 \end{gathered}$

Consider that the area of the circle with diameter (d) is given by,

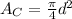
$A_C=(\pi)/(4)d^2$

According to the given problem,

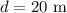
$d=20\text{ m}$

Then the area of the circle becomes,

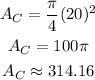
$\begin{gathered} A_C=(\pi)/(4)(20)^2 \\ A_C=100\pi \\ A_C\approx314.16 \end{gathered}$

Now, the area of the shaded region (A) is calculated as,

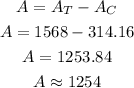
$\begin{gathered} A=A_T-A_C \\ A=1568-314.16 \\ A=1253.84 \\ A\approx1254 \end{gathered}$

Thus, the area of the shaded region is 1254 sq. meters approximately.

Therefore, the 3rd option is correct choice.