How would i answer and what would be the answer?

Question

asked Nov 21, 2023 198k views

1 Answer

Sony · Answer 1 · 2023-11-27T19:57:55+0000

Given

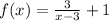
The vertical asymptotes are given by the value of x which makes the denominator equal to zero. In our case,

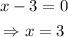
$\begin{gathered} x-3=0 \\ \Rightarrow x=3 \end{gathered}$

Thus, the vertical asymptote is x=3.

As for the horizontal asymptote, notice that

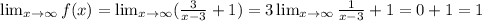
$\lim _(x\to\infty)f(x)=\lim _(x\to\infty)((3)/(x-3)+1)=3\lim _(x\to\infty)(1)/(x-3)+1=0+1=1$

Similarly,

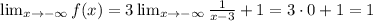
$\lim _(x\to-\infty)f(x)=3\lim _(x\to-\infty)(1)/(x-3)+1=3\cdot0+1=1$

Therefore, the horizontal asymptote is y=1.

As for the domain of the function, the only points that are not included in the domain are those that cause a vertical asymptote. Hence,

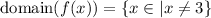
$\text{domain}(f(x))=\mleft\lbrace x\in\R|x\\e3\mright\rbrace$

Similarly, since y=1 is a horizontal asymptote,

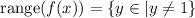
$\text{range}(f(x))=\mleft\lbrace y\in\R|y\\e1\mright\rbrace$

Thus, the domain is all real numbers except 3, and the range is all real numbers except 1.