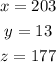The sum of three integers is 393. The sum of the first and second integers exceeds the third by39. The third integer is 26 less than the first. Find the three integers.

Question

asked Sep 3, 2023 136k views

1 Answer

Ubeogesh · Answer 1 · 2023-09-09T18:52:05+0000

For the given question, let the numbers are = x, y, and z

The sum of three integers is 393 ⇒ x + y + z = 393

The sum of the first and second integers exceeds the third by 39

so, x + y - z = 39

The third integer is 26 less than the first.

So, x - 26 = z

So, we have the following system of equations:

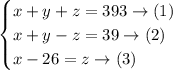
$\begin{cases}{x+y+z=393\rightarrow\left(1\right)} \\ {x+y-z=39\rightarrow\left(2\right)} \\ {x-26=z\rightarrow\left(3\right)}\end{cases}$

Substitute with (z) from equation (3) into equation (2):

$\begin{gathered} x+y-\left(x-26\right)=39 \\ x+y-x+26=39 \\ y=39-26=13 \end{gathered}$

substitute with (y) into the equations (1) and (2)

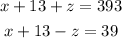
$\begin{gathered} x+13+z=393 \\ x+13-z=39 \end{gathered}$

Add the equations to eliminate (z) then solve for (x):

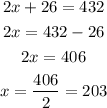
$\begin{gathered} 2x+26=432 \\ 2x=432-26 \\ 2x=406 \\ x=(406)/(2)=203 \end{gathered}$

substitute with (x) into equation (3) to find (z)

so, the answer will be:

$\begin{gathered} x=203 \\ y=13 \\ z=177 \end{gathered}$