Question

Selected three sides length that can form a right triangle

Answer 1

Various possible side lengths of a right triangle are given.

It is required to choose which three will truly form a right triangle.

Recall the Pythagorean Theorem:

The Pythagorean Theorem states that in a right triangle, the relationship between the lengths of legs a and b and the length of the hypotenuse c is:

`a^2+b^2=c^2`

Check any three side lengths given. Notice that:

`\begin{gathered} 12^2+35^2=37^2 \\ \Rightarrow144+1225=1369 \\ \Rightarrow1369=1369 \end{gathered}`

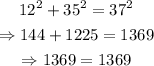
This implies that the three side lengths, 12, 35, and 37 satisfy the Pythagorean triple.

Hence, the three side lengths that can form a right triangle are 12 units, 35 units, and 37 units.

Select 12 units, 35 units, and 37 units.