Question

Solving a distance rate time problem using a system of linear equations

Answer 1

`\begin{gathered} \text{ Rate of the boat in still water }=36mi\/hr \\ \text{ Rate of the current }=9mi\/hr \end{gathered}`

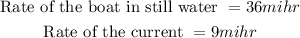
Step-by-step explanation

We want to find the rate of the boat in still water and the rate of the current.

Let the boat's rate be x.

Let the rate of the current be y.

When the boat is traveling upstream, it means that it is traveling against the current. This implies that its rate traveling upstream is:

`x-y`

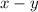
Using the relationship between speed (rate) and distance, we can write that for the upstream travel:

`\begin{gathered} s=(d)/(t) \\ \Rightarrow x-y=(108)/(3) \\ x-y=36 \end{gathered}`

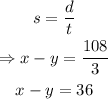
When the boat is traveling downstream, it means that it is traveling along with the current. This implies that its rate traveling downstream is:

`x+y`

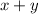
and:

`\begin{gathered} x+y=(108)/(2) \\ x+y=54 \end{gathered}`

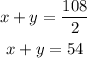
Now, we have two simultaneous linear equations:

`\begin{gathered} x-y=36 \\ x+y=54 \end{gathered}`

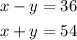
Solve for x by elimination. To do this, add the two equations and simplify:

`\begin{gathered} x-y+x+y=36+54 \\ 2x=90 \\ x=(90)/(2) \\ x=45mi\/hr \end{gathered}`

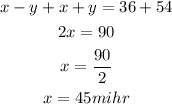
Solve for y by substituting x into the second equation:

`\begin{gathered} 45+y=54 \\ \Rightarrow y=54-45 \\ y=9mi\/hr \end{gathered}`

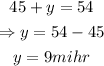
Hence, the rate of the boat in still water is 36 mi/hr and the rate of the current is 9 mi/hr.