Question

Use the given right triangle to find ratios, inreduced form, for sin A, cos A, and tan A.

Answer 1

In the given right triangle,

BC=5

AC=12.

Hypotenuse of the triangle, AB=13.

Now, the ratio of sin A can be expressed as,

`\sin A=\frac{opposite\text{ side}}{hypotenuse}`

The opposite side to angle A is BC.

Hence,

`\begin{gathered} \sin A=(BC)/(AB) \\ \sin A=(5)/(13) \end{gathered}`

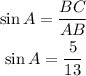
The ratio of cos A can be expresssed as,

`\cos \text{ A=}\frac{\text{adjacent side}}{hypotenuse}`

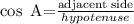
The side adjacent to angle A is AC.

Hence,

`\begin{gathered} \cos \text{ A=}(AC)/(AB) \\ \cos \text{ A=}(12)/(13) \end{gathered}`

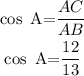
The ratio tan A can be expressed as,

`\begin{gathered} \tan \text{ A=}\frac{\text{opposite side}}{adjacent\text{ side}} \\ \tan \text{ A=}(BC)/(AC) \\ \tan \text{ A=}(5)/(12) \end{gathered}`

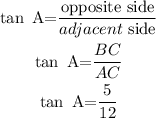
Therefore, sin A=5/13, cos A=12/13 and tan A=5/12.