Question

A box contains 5 balls. Two are numbered 3, one is numbered 4,and two are numbered 5. The balls are mixed and one is selected at random. After a ball is selected,it’s number is recorded. Then it is replaced. If the experiment is repeated many times. Find the variance and standard deviation of the numbers on the balls.

Answer 1

Let X be the number on each ball. The probability distribution is:

now, the mean is

`\mu=\sum_^X\text{ . P\lparen X})`

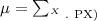
According to the data, this Mean would be:

`\mu=\sum_^X\text{ . P\lparen X})\text{ }=\text{ 3 . }(2)/(5)\text{ }+4\text{ . }(1)/(5)\text{ }+5\text{ . }(2)/(5)\text{ }=4`

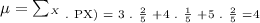
So, we get that the Mean is:

`\mu=4`

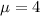
Now, the variance is

`\sigma\text{ }=\text{ }\sum_^\lbrack X^2\text{ . P\lparen X})\rbrack-\mu^2`

According to the data of the problem, we get that the variance is:

`\sigma=\text{ }\lbrack\text{3}^2\text{ . }(2)/(5)\text{ }+4^2\text{ . }(1)/(5)\text{ }+5^2\text{ . }(2)/(5)\text{ }\rbrack\frac{}{}-4^2`

this is equivalent to:

`\sigma=(4)/(5)`

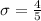
Thus, the standard deviation would be:

`\sqrt{(4)/(5)}=0.894`

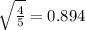
Then, we can conclude that the correct answer is:

Variance:

`(4)/(5)`

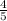
Standard deviation:

`0.894`