Question

Given the focus and directrix shown on the graph what is the vertex form of the equation of the parabola?

Answer 1

The equation of the directrix is x = -4 and the focus coordinates are (1, 3).

Since the directrix is a vertical line, we can use the model below for a parabola that opens to the right or left:

`(y-k)^2=4p(x-h)`

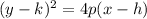
Where the focus is located at (h + p, k) and the directrix is x = h - p.

Since the directrix is x = -4 and the focus is (1, 3), we have:

`\begin{gathered} h+p=1 \\ h-p=-4 \\ k=3 \end{gathered}`

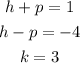
Adding the first two equations, we have:

`\begin{gathered} 2h=-3 \\ h=-(3)/(2) \\ \\ h+p=1 \\ -(3)/(2)+p=1 \\ p=(5)/(2) \end{gathered}`

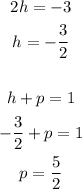
Therefore the equation is:

`(y-3)^2=10(x+(3)/(2))`

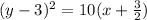
Now, let's rewrite it in the vertex form:

`\begin{gathered} vertex\text{ }form\to x=a(y-k)^2+h \\ \\ (y-3)^2=10(x+(3)/(2)) \\ (1)/(10)(y-3)^2=x+(3)/(2) \\ x=(1)/(10)(y-3)^2-(3)/(2) \end{gathered}`

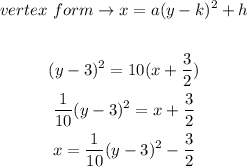
Therefore the correct option is A.