Question

How does the value of the eccentricity of the ellipse describe its shape?

Answer 1

Given:

The given equation is:

`(x^2)/(16)+(y^2)/(80)=1`

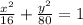
Required:

Find how the value of the eccentricity describes the shape of the ellipse.

Find the value of the eccentricity.

Step-by-step explanation:

If the value of the eccentricity is less than one the shape of the figure will be an ellipse that the eccentricity of the ellipse is less than 1.

Rewrite the given equation as:

`(x^2)/((4)^2)+(y^2)/((4√(5))^2)=1`

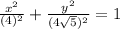
Compare the given equation with the standard equation of the ellipse

`(x^2)/(a^2)+(y^2)/(b^2)=1`

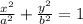
We get

`a=4\text{ and b =4}√(5)`

Here b>a so the major axis will be y and the minor axis will be x.

The eccentricity is given by the formula:

`e=\sqrt{1-(a^2)/(b^2)}`
`\begin{gathered} e=\sqrt{1-(16)/(80)} \\ e=\sqrt{1-(1)/(5)} \\ e=(2)/(√(5)) \\ e=(2)/(2.236) \\ e=0.8944 \\ e\approx0.89 \end{gathered}`

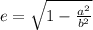
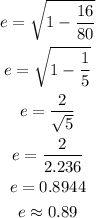
This value indicates that the ellipse is elongated than circular.

Final Answer:

The value of e =