Question

Triangle LRG is similar to Triangle CNP. Find the scale factor required to dilate triangle LRG so that its image is is congruent to triangle CNP.

Answer 1

Triangle LRG is similar to triangle CNP. Therefore, the following ratios apply;

`\begin{gathered} (CN)/(LR)=(PN)/(GR) \\ \text{Similarly,} \\ (CP)/(LG)=(PN)/(GR) \end{gathered}`

Hence, for triangle LRG to be dilated to become CNP,

`\begin{gathered} (45)/(30)=(48)/(32) \\ (3)/(2)=(3)/(2) \end{gathered}`

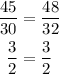
Therefore, the scale factor needed to dilate triangle LRG so that its image is congruent to triangle CNP is 1.5 (that is the decimal equivalent of 3/2)

This means triangle LRG would be multiplied by 1.5 in order to have an image congruent to triangle CNP