Question

Calculate the difference quotients for H(x) = 1/5*x*x – 2 using h = 0.1,0.01, and 0.001. Use the results to approximate the slope of the tangent line to the graph ofH(x) at the point (5.3). If necessary, round the difference quotients to no less than six decimal places and round your final answer to the nearest integer.

Answer 1

For h=0.1 the difference quotient of the given function is:

`\begin{gathered} (H(x+0.1)-H(x))/(0.1)=((1)/(5)(x+0.1)^2-2-(1)/(5)x^2+2)/(0.1) \\ =2(x+0.1)^2-2x^2=2((x+0.1)^2-x^2)=2(x+0.1+x)(x+0.1-x) \\ =2(2x+0.1)(0.1)=0.4x+0.02. \end{gathered}`

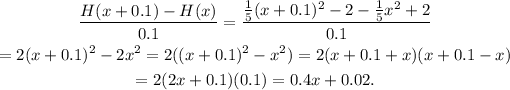
For h=0.01 the difference quotient of the given function is:

`\begin{gathered} (H(x+0.01)-H(x))/(0.01)=((1)/(5)(x+0.01)^2-2-(1)/(5)x^2+2)/(0.01) \\ =20(x+0.01)^2-20x^2=20((x+0.01)^2-x^2)=20(x+0.01+x)(x+0.01-x) \\ =20(2x+0.01)(0.01)=0.4x+0.002. \end{gathered}`

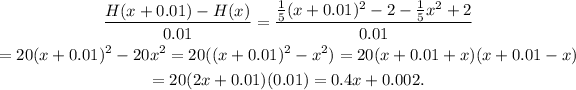
For h= 0.001 the difference quotient of the given function is:

`\begin{gathered} (H(x+0.001)-H(x))/(0.001)=((1)/(5)(x+0.001)^2-2-(1)/(5)x^2+2)/(0.001) \\ =200(x+0.001)^2-200x^2=200((x+0.001)^2-x^2)=200(x+0.001+x)(x+0.001-x) \\ =200(2x+0.001)(0.001)=0.4x+0.0002. \end{gathered}`

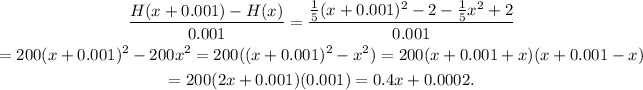
Substituting x= 5 in each quotient we get:

`\begin{gathered} 0.4(5)+0.02=2.02, \\ 0.4(5)+0.002=2.002, \\ 0.4(5)+0.0002=2.0002. \end{gathered}`

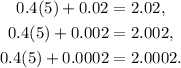
Answer:

Slope of the tangent line: 2.